Област дефинисаности функције


Нека су А и В два непразна скупа. Пресликавање (или функција) скупа А у скуп В, у ознаци f: А → В је придруживање елемената скупова А и В тако да сваком елементу скупа А одговара тачно један елеменат скупа В. Скуп А се назива домен (област дефинисаности) функције. Скуп В се назива кодомен (област вредности) функције. Скуп слика (скуп врдности) функције је подскуп кодомена и чине је они елементи кодомена у које се пресликао барем један елеменат домена.

Нека је дата функција f: D → V (D,V R). Област дефинисаности реалне функције y=f(x) је скуп реалних вредности независне променљиве x за које је вредност функције реална.



Одредити област дефинисаности следећих функција:

Пример 1.



Израз под кореном мора бити ненегативан




■


Пример 2.





Претходна неједначина се може решити тако што се направи табела знакова за сваки од израза и затим се одреди знак разломка.

Изрази могу променити знак само у својим нулама, зато се одреде вредности    за које су изрази једнаки нули.





Знак израза може да се одреди тако што се реши неједначина  ,  или тако што се замени нека вредност за x. Израз    је за    негативан, па мора бити истог знака тј. негативан на целом интервалу . Слично, израз    је за    негативан, па је негативан на интервалу  .



Плусеви у табели значе да је израз позитиван, а минуси да је израз негативан. Домен дате функције је



■


Пример 3.

а)  








б)  



Знак производа се може одредити као и знак разломка помоћу табеле. Практично је и обележити производ са и у табели уписати A уместо производа.





■


Пример 4.







Одређивање знака квадратног тринома је рађено у другом разреду и потребно је подсетити се. Прво се одреде решења једначине



Знак тринома се прочита са скице графика квадратне функције одређене тим триномом као на слици




Именилац разломка мора бити различит од нуле. Реши се одговарајућа једначина и искључе се нуле.





Домен функције је пресек ова два скупа.



■


Пример 5.









Трином из имениоца има негативан број уз квадратни члан па је одговарајућа скица за знак









■


Пример 6.








■


Пример 7.






■


Пример 8.












■


Пример 9.

















■


Пример 10.







■

Скуп вредности функције


Област вредности (скуп слика, скуп врдности) функције је подскуп кодомена и чине је они елементи кодомена у које се пресликао барем један елеменат домена (скуп вредности y за које постоји x).




Одредити област вредности функције:

Пример 1.










■

Пример 2.


Своођењем функције на канонски облик добија се










■

Пример 3.




Решавањем једнакости (*) по x добиће се квадратна једначина





Да би једначина имала реална решења по x (домен функције је скуп R), дискриминанта једначине мора бити већа или једнака од нуле, па следи










■

Пример 4.






■

Пример 5.






■

Пример 6.






■

Пример 7.






■

Ограниченост функцијe

Функција f: D → F (D,F R) је ограничена одозго ако постоји реалан број M тако да за свако x из домена је f(x)<=M, тј:
                                           

Функција f: D → F (D,F R) је ограничена одоздо ако постоји реалан број m тако да за свако xЄD је f(x)>=m, тј:

                                           

Функција f: D → F (D,F R) је ограничена ако је ограничена одозго и одоздо.

                                   

Пример 1.





функција је ограничена.
■

Пример 2.





■


Парност и непарност функција

Функција f: D → F (D,F R) је парна ако за свако x Є D је .

Функција f: D → F (D,F R) је непарна ако за свако x Є D је .

Ако је , тада функција није ни парна ни непарна.

График парне функције је симетричан у односу на y осу, а график непарне функције је симетричан у односу на координатни почетак. Домени парних/непарних функција су симетрични у односу на тачку x=0.

Парност/непарност функције и периодичност се проверавају после одређивања домена (пре осталих особина). Ако је функција парна или непарна онда је довољно испитати је на интервалу и симетрично пресликати особине и график на интервал .



Пример 1.




Функција је непарна.
■


Пример 2.




Функција је парна.
■


Пример 3.






Функција није ни парна ни непарна.
■


Пример 4.




Домен функције је асиметричан па функција није ни парна ни непарна (није потребно испитивати парност/непарност).

■


Пример 5.




Функција је непарна.
■


Пример 6.




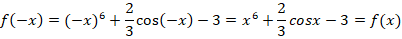
Функција је парна.
■


Пример 7.




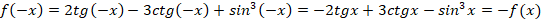
Функција је непарна.
■


Пример 8.




  (домен је симетричан)



Функција је непарна.
■


Пример 9.




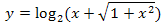
функција је непарна.
■

Периодичност функција


Функција f: D → F (D,F R) је периодична ако


Најмањи број Т који испуњава претходни услов је основни период функције.

Пример 1.







■

Пример 2.



■


Нуле и знак функција


Нула функције f: D → F (D,F R) је сваки реалан број x0 Є D за који је f(x0) = 0. Нуле функције се одређују решавањем једначине f(x) = 0.

Знак функције се одређује решавањем неједначине f(x) > 0, или f(x) < 0.



Пример 1.



Знак ове функције је одређен при одређивању домена функције    у примеру 5.

Одреде се нуле бројиоца



Знак бројиоца



Одреде се нуле имениоца



Трином из имениоца има негативан број уз квадратни члан па је одговарајућа скица за знак



Скицира се табела знакова





Знак функције се прочита из табеле





Нуле функције су нуле бројиоца



■




Пример 2.



Одреди се домен функције из табеле знакова разломка под кореном







Особине функције се испитују само на домену, па функција не може имати негативних вредности



Нуле функције су



■


Пример 3.



Дата функција је дефинисана за сваки реалан број.

Ако је изложлац корена непаран онда израз под кореном може бити и негативан и позитиван и једнак нули, а ако је изложилац корена паран број онда израз под кореном мора бити ненегативан.





Израз    је позитиван осим за  .









■


Пример 4.



Дефинисаност израза   зависи од израза  .

Израз     је дефинисан за  .



Израз    је увек позитиван .

Знак функције је исти као знак тринома  .







■


Пример 5.



Логаритам је дефинисан ако је израз под логаритмом позитиван, тј.















■

Монотоност функција


За функцију f: D → F (D,F R) кажемо да је:

1o   растућа ако ;
2o   опадајућа ако ;
3o   нерастућа ако ;
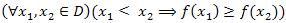
4o   неопадајућа ако .

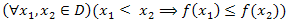
Ако је функција нерастућа или неопадајућа кажемо да је монотона, а ако је растућа или опадајућа онда кажемо да је функција строго монотона.




Сложена функција (каже се и производ ф-ја, композиција ф-ја)


Нека су дате функције  



Нека је  

Тада је  

Функција     је сложена функција и важи





Пример 1.

Дате су реалне функције

.

Одредити .





■